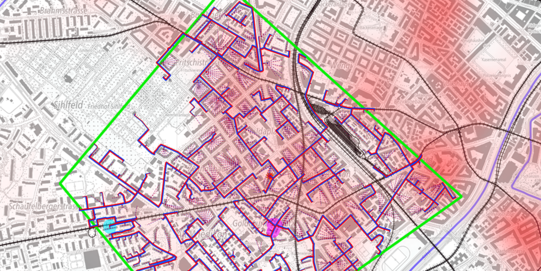
Automatische Fernwär­menetz-Generierung

Mathematiker entwickeln seit Jahrzehnten Algorithmen, die verschiedene Berechnungen innerhalb der Graphen durchführen können. Ein bekanntes Problem ist es, den kürzesten Weg zwischen zwei zusammen­hängenden Knoten zu finden. Eine Variante davon wird beispielsweise jedes Mal angewendet, wenn Sie eine Route in Google Maps eingeben. Auch Fernwärmenetze (oder Netze im Allgemeinen, beispielsweise Abwasserleitungen) lassen sich sehr gut als Graphen darstellen. Übrigens gibt es sogar sogenannte Minimal-Flow-Probleme, das aber für ein anderes Mal. Da wir diese Fernwärmenetze also plötzlich mathematisch und ohne Inter­pre­ta­tionsspiel­raum abbilden können, ermöglicht uns das automatisch, ein Fernwärmenetz zu er­stellen. Alles, was wir dafür vom Nutzer benötigen, ist ein gewünschtes Gebiet und eine soge­nannte Quelle, also ein Ausgangspunkt. Der Algorithmus berechnet dann automatisch ein optimales Fern­wärme­netz. Dieses hält gewisse Bedingungen (wie Strassen, Priorisierung etc.) ein und wird im QGIS oder jeder anderen Geo-Software visualisiert. Was hier «optimal» bedeu­tet, ist natürlich zuerst zu definieren; in unserem Beispiel werden die geringsten Kosten berechnet.

Wir haben gesehen also, dass eine mathematisch rigorose Definition des Problems unum­gäng­lich ist. Dies ist einem vielleicht nicht immer bewusst, aber wenn man etwas mit Software auto­ma­tisieren möchte, ist das Problem sehr häufig mathematisch beschreibbar. Neben der Mathe­ma­tik ist natürlich auch die Verfügbarkeit offener Daten extrem wichtig. Auch wenn einige Informa­tionen aus unserem Internen Fundus stammen, wäre eine Umsetzung ohne Open-Source-Daten un­möglich. Was die Softwarekomponenten betrifft, setzen wir praktisch aus­schliess­lich auf Open Source.